马赫-曾德尔干涉仪(Mach-Zehnder interferometer)是一种干涉仪。可以用来观测从单独光源发射的光束分裂成两道准直光束(Collimated beam)之后,经过不同路径与介质所产生的相对相移变化。
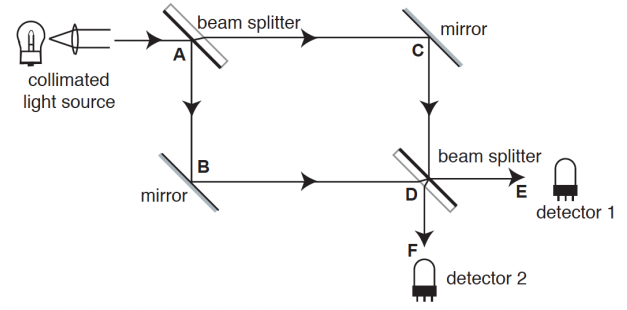
其中,分光镜是干涉仪的重要组件。在马赫-曾德尔干涉仪中,假若波动从空气传播遇到镜子表面的镀膜,则反射波的相移为$\pi$;若波动从从镜子后部的玻璃传播遇到镜子表面的镀膜,则反射波的相移为$0$。另外假若通过镜子后部的玻璃会造成常数相移$k$,则从镜子后部的玻璃遇到镜子表面的镀膜反射回来所遭到的相移为$2k$。
由于一束光在分束器的每次反射/透射中,光束的能量都会分成两部分。 因此反射波的强度与入射波的强度之比称为半反射表面的反射率$\mathcal{R}$。
$$
\begin{align}
\mathcal{R}\equiv \dfrac{I_\text{ reflected wave}}{I_\text{ incident wave}} = \left(\dfrac{A_\text{ reflected wave}}{A_\text{ incident wave}}\right)^2\equiv r^2
\end{align}
$$
根据能量守恒可以得出
$$
\begin{align}
\dfrac{I_\text{ trensmitted wave}}{I_\text{ incident wave}} = \left(\dfrac{A_\text{ trensmitted wave}}{A_\text{ incident wave}}\right)^2\equiv (1-\mathcal{R})
\end{align}
$$
理想情况下反射率为$50%$。
空间中任何一点的电磁波的相位随着波传播路径的长度线性变化。当电磁波在离开某个参考点后,沿路径长度$L$传播时,其相位变化等于传播路径长度$L$与波长$\lambda$之比。
$$
\begin{align}
\Delta\phi = 2\pi\dfrac{L}{\lambda} = 2\pi\dfrac{nL}{\lambda_0}
\end{align}
$$
其中$\lambda_0$为真空中的波长,$n$为折射率。
设通过镜子后部的玻璃造成常数相移$k=0$,假设初始光束于时间$t$在起点的电场为
$$
\begin{align}
E_{0,A}(t)=A_0\cos(\omega t)
\end{align}
$$
那么在 E 点到达探测器 1 的两束光束的电场(第一束沿路径 ACDE 传播,第二束沿 ABDE 传播)分别为
$$
\begin{align}
E_{1,E}(t)=A_0\sqrt{(1-\mathcal{R})\mathcal{R}}\cos(\omega t-2\pi\dfrac{nL_{ACDE}}{\lambda_0}-2\pi)
\end{align}
$$
$$
\begin{align}
E_{2,E}(t)=A_0\sqrt{\mathcal{R}(1-\mathcal{R})}\cos(\omega t-2\pi\dfrac{nL_{ABDE}}{\lambda_0}-2\pi)
\end{align}
$$
同样的,在点 F 到达检测器 2 并沿 ACDF 和 ABDF 传播的两个光束的电场为分别为
$$
\begin{align}
E_{3,F}(t)=A_0(1-\mathcal{R})\cos(\omega t-2\pi\dfrac{nL_{ACDF}}{\lambda_0}-\pi)
\end{align}
$$
$$
\begin{align}
E_{4,F}(t)=A_0\mathcal{R}\cos(\omega t-2\pi\dfrac{nL_{ABDF}}{\lambda_0}-2\pi)
\end{align}
$$
从Eqs.(5)-(8)可以看出,如果两条路径的折射率不同,则探测器处是否存在相消干涉或相长干涉将敏感地取决于该差异。同时这也意味着马赫-曾德干涉仪的探测器的输出对其光束行进的光路长度要求极其严格。如果任一臂的长度仅变化半个波长,则强度可以从最大值变为最小值,因此两条光路的长度必须严格相等。
因此可以使用马赫-曾德尔干涉仪的拓扑构造光子器件,其中各种光导(例如光纤)作为两个臂。 平面波的初始光束(振幅$1.0$和强度$0.5$单位)在Y-结处分成两个相等的光束(振幅$0.71$和强度$0.25$单位)。它们沿着两个不同的光导向前移动,然后在第二个Y-结处再次聚集成一束光,其幅度和强度根据两个臂的路径长度而变化。在一些透明材料中,即所谓的电光晶体,可以通过施加外部电场来改变晶体折射率。因此,通过改变晶体两侧的电场以改变其中光的相位,进而控制汇集时两束光的干涉方式。简而言之,合成的光信号将是一个通过控制其偏置电压而改变其强度大小的干涉信号。
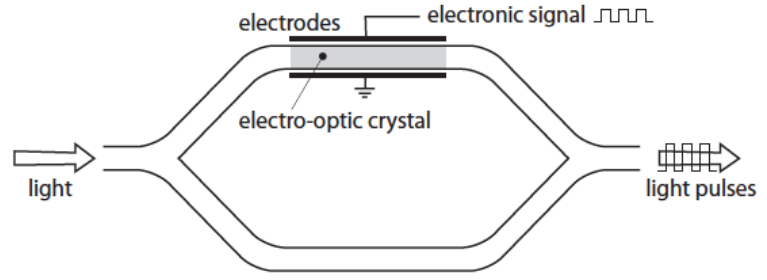
显然,如果电场的作用是将光程长度增加$\{x \vert x=n,n\in\displaystyle Z\}$个波长,则输出光束将具有与输入光束相同的强度。而如果增加$\{x \vert x=n+0.5,n\in\displaystyle Z\}$个波长,则检测器将不会检测到光束。上述的电光特性称为普克尔斯效应。由$n \approx n_1+pE$表示折射率$n$作为电场$E$的函数。
另一种可选的材料为压电材料,长度公式为$\dfrac{\Delta l}{l} \approx KE$。其长度在施加外电场时会略微发生变化,因此也可以作为马赫-曾德尔调制器中的移相部件。